মার্ক টোয়েন একটি কথা বলে অনেক বিখ্যাত হয়েছিলেন । তিনি বলেছিলেন সত্যকে অস্বীকার করার তিনটি উপায় রয়েছে : মিথ্যা কথা , ডাহা মিথ্যা কথা এবং পরিসংখ্যান ।
মার্ক টোয়েন এর এই বিখ্যাত উক্তিটি সর্বতো ভাবে সত্য।
খুব কম জনই সঠিক ভাবে স্ট্যাটিস্টিক্সের প্রয়োগ পদ্ধতি
জানেন কাজেই সাধারণভাবেই স্ট্যাটিস্টিক্সের সহায়তায় মিথ্যা বলা সম্ভব।
জর্জ কর্লিন এক বার বলেছিলেন
Think about how stupid the average person is;
now realize half of them are dumber than that.
খুব কম জনই সঠিক ভাবে স্ট্যাটিস্টিক্সের প্রয়োগ পদ্ধতি
জানেন কাজেই সাধারণভাবেই স্ট্যাটিস্টিক্সের সহায়তায় মিথ্যা বলা সম্ভব।
জর্জ কর্লিন এক বার বলেছিলেন
Think about how stupid the average person is;
now realize half of them are dumber than that.
একটা উদাহরণ দিলে স্ট্যাটিস্টিক্সের অপপ্রয়োগের ব্যাপারটি পরিষ্কার হবে:
মহিলারা পুরুষদের তুলনায় ভালো ড্রাইভার : দুর্ঘটনার জন্য দায়ী অথবা দুর্ঘটনাগ্রস্ত গাড়ির ড্রাইভারের সংখ্যার তুলনামূলক বিচার করলে হয়তো দেখা যাবে সত্যিই মহিলা ড্রাইভারের হাতে দুর্ঘটনা কম হয়েছে। কিন্তু এখানে একটি তথ্য পরিবেশন করা হচ্ছে না যে মহিলা ড্রাইভারের সংখ্যা (যাঁরা নিয়মিত গাড়ি নিয়ে বেড়োন) পুরুষ ড্রাইভারের সংখ্যার তুলনায় নগণ্য।সে জন্য এখানে এই তথ্য মিথ্যা।
ডেটা এনালাইসিস করার আগে অন্তত প্রাথমিক বিষয় গুলো বোঝা খুবই গুরুত্বপূর্ণ।
প্রাথমিক বিষয় গুলোর মধ্যে সবচেয়ে গুরুত্বপূর্ণ বিষয় হলো Central Limit Theorem
প্রাথমিক বিষয় গুলোর মধ্যে সবচেয়ে গুরুত্বপূর্ণ বিষয় হলো Central Limit Theorem
"Central Limit Theorem" পরিসংখ্যানের একটি গুরুত্বপূর্ণ থিওরেম বা উপপাদ্য।
"Central Limit Theorem" অনুসারে যখন Sample Size যথেষ্ট বড় হয়
( সাধারণত ৩০ বা তার অধিক) Variable বা চলক যে Population থেকেই
নেওয়া হোক না কেন, চলকটির গড় (Mean) এর স্যাম্পলিং ডিট্রিবিউশনটি
approximately নরমাল ডিষ্ট্রিবিউশন ফলো করবে।
সংগাটি যদি আমরা একটু ব্যাখ্যা করে বলতে যাই,
তাহলে প্রথমেই বলতে হয় যেকোন Population বলতে Central limit theorem
এ কি বুঝায়?
আসলেই কি সব Population Distribution এর ক্ষেত্রেই
এই উপপাদ্যটি প্রযোজ্য?
আমরা জানি, আমরা যে স্যাম্পল বা নমুনা নিয়ে কাজ করবো
সেটা যেকোন Population থেকে আসতে পারে।
পরিসংখ্যানের সবগুলো ডিস্ট্রিবিউশনকে আমরা তাদের
Shape বা আকৃতি অনুসারে প্রধানত মোট চারটি ভাগে
ভাগ করতে পারি।
1. Normal
"Central Limit Theorem" অনুসারে যখন Sample Size যথেষ্ট বড় হয়
( সাধারণত ৩০ বা তার অধিক) Variable বা চলক যে Population থেকেই
নেওয়া হোক না কেন, চলকটির গড় (Mean) এর স্যাম্পলিং ডিট্রিবিউশনটি
approximately নরমাল ডিষ্ট্রিবিউশন ফলো করবে।
সংগাটি যদি আমরা একটু ব্যাখ্যা করে বলতে যাই,
তাহলে প্রথমেই বলতে হয় যেকোন Population বলতে Central limit theorem
এ কি বুঝায়?
আসলেই কি সব Population Distribution এর ক্ষেত্রেই
এই উপপাদ্যটি প্রযোজ্য?
আমরা জানি, আমরা যে স্যাম্পল বা নমুনা নিয়ে কাজ করবো
সেটা যেকোন Population থেকে আসতে পারে।
পরিসংখ্যানের সবগুলো ডিস্ট্রিবিউশনকে আমরা তাদের
Shape বা আকৃতি অনুসারে প্রধানত মোট চারটি ভাগে
ভাগ করতে পারি।
1. Normal



Central Limit Theorem প্রায় সব ধরনের Distribution
এর ক্ষেত্রেই প্রয়োগ করা যায়। কিন্তু কিছু ব্যতিক্রমও রয়েছে।
উদাহরণ হিসেবে বলা যেতে পারে Population এর Variance
অবশ্যই সসীম হতে হবে।
যেমন Cauchy distribution এর কথা বলা যেতে পারে। Cauchy distribution
এর কোন Mean নেই এবং
Variance ও অসীম। এক কথায় এর সংগায়িত
কোন Mean বা Variance নেই।
আবার Central Limit Theorem শুধুমাত্র identically
এবং independently distributed চলক এর ক্ষেত্রে
ব্যবহার করা যাবে। মানে একটি অবজারবেশন এর মান
যদি অন্য আর একটি অবজারবেশন এর উপর নির্ভর করে
সেক্ষেত্রে আমরা Central Limit Theorem এর প্রয়োগ করতে পারবো না।
এবার আসি Sampling Distribution of Mean বলতে আমরা আসলে কি বুঝি?
মনে করুন একটি স্টাডি এর আন্ডারে আপনি কিছু নমুনা সংগ্রহ করলেন
এবং এর গড় মানটি বের করলেন।
এবং মনে করুন আপনি ওই একই স্টাডি এর আন্ডারে একই সাইজের আরো কিছু স্যাম্পল
বা নমুনা সংগ্রহ করলেন
এবং সেগুলোর গড় মান বের করলেন। এভাবে কয়েকবার রিপিট করলেন।
এবার আপনি যদি এই প্রত্যেকটি নমুনার গড় নিয়ে Histogram আঁকেন
তাহলে আপনার এই হিস্ট্রোগ্রামটি
একটি ডিষ্ট্রিবিউশন এর Shape প্রদর্শন করবে এবং
এই ডিষ্ট্রিবিশনকেই পরিসংখ্যানবিদরা বলেন
Sampling Distribution of Mean.
আশার কথা হচ্ছে, Mean এর Sampling Distribution বের করার জন্যে
আমাদের স্টাডিটা অনেকবার রিপিট করার
প্রয়োজন পরে না। পরিসংখ্যানের পদ্ধতি একটি
একক দৈব নমুনা( Random variable) থেকেই এটি Estimate
বা অনুমান করতে পারেন।
এবার আসি Sample Size এর সাথে Central Limit Theorem (CLT)
এর সম্পর্কটা আসলে কি?
Smaple Size পরিবর্তনের সাথে সাথে Sampling Distribution
এর Shape বা আকৃতি এরও পরিবর্তন ঘটে।
Central Limit Theorem (CLT) এর সংগানুসারে Sample Size
বাড়ালে Mean এর
Sampling Distribution Approximately Normally Distributed হবে।
কিন্তু কত বাড়ালে?
এটা আসলে নির্ভর করে চলকটি যেই Population থেকে আসবে
তার Distribution এর Shape এর উপর।
"The more the population distribution differs from being normal,
the larger the sample size must be"
অনেক Statistician এর মতে বেশিরভাগ Distribution এর ক্ষেত্রে
Sample size 30 হলেই যথেষ্ট।
কিন্তু Strongly Skewed Distribution এর জন্যে
৩০ এর অধিক Sample এর প্রয়োজন।
CLT দুইটি বিষয়ের একের সাথে অপরের লিংক-আপ করে। এই দুটি বিষয় হলো
1. চলকটির Population এর Distribution এবং
2. গড়( Mean) এর Sampling Distribution
CLT বলে চলকটির Population এর Distribution যাই হোক না
কেন তার গড়( Mean)
এর Sampling Distribution Approximately Normally
Distributed হবে।
এখানে Normally Distributed হবে মানে কি?
মানে মনে করুন Population Distribution এর Shape
নিচের মত আছে
আমরা জানি Normal Distribution এর দুইটি প্যারামিটার আছে
Mean এবং Variance।
এখন কথা হচ্ছে Mean এর Sampling Distribution
যখন Normally Distributed হবে তখন Mean এবং Variance
কি হবে?
CLT এর Property বলে Mean এর Sampling Distribution Approximately Normally Distributed হবে
যার Mean হবে Population Mean এর সমান এবং Variance হবে σ^2/n
যেখানে,
σ^2= the population variance and
n = the sample size
তাহলে আমি যদি Sample Size বাড়াতে থাকি তাহলে অবশ্যই
Variance এর মান কমতে থাকবে এর মানে
Standard deviation এর মানও কমতে থাকবে
কারণ variance এর ডিনোমিনেটর হিসেবে n বা Sample size রয়েছে।
এর Scale Parameter আর Scale Parameter এর কাজই হলো
Distribution এর Shape কি রকম Spread বা বিস্তৃত হবে তা নির্ধারণ করা।
Standard Deviation বা Variance যত বেশী হবে Distribution এর
Shape তত বিস্তৃত হবে অতএব Sample Size বাড়ানোর সাথে সাথে
Mean এর Sampling Distribution এর Standard Deviation এর
মান যেহেতু কমবে সেহেতু Distribution এর Shape এর বিস্তৃতি কমে
Mean এর কাছাকাছি আসতে থাকবে এবং এটা Normal Distribution
এর Shape এর মতো দেখাবে।

মনে করুন আপনি একটি ছক্কার গুটি অনেকবার রোল করলেন।
যেহেতু ১-৬ প্রত্যেকটি সংখ্যা আসার
সম্ভাবনা ১/৬ = ০.১৬৬৭ আমরা আশা করবো প্রত্যেকটি সংখ্যা
আসার প্রোপোরশন সমান হবে বানে ০.১৬৬৬৬৭
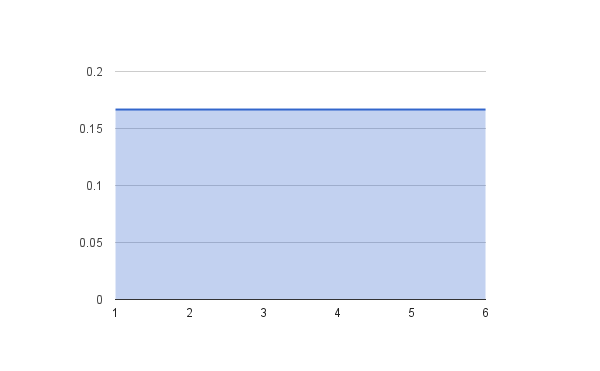
এরপর একই কাজটি ২ টি ছক্কার গুটি দিয়ে করুন।
খেয়াল করে দেখুন তাদের যোগফল ২ অথবা ১২ কেবল মাত্র ১টি উপায়েই হতে পারে।
মানে ১+১ = ২ বা ৬+৬ = ১২। তাহলে ২ বা ১২ আসার সম্ভাবনা ১/৩৬=০.০২৭।
কিন্তু ৭ অনেকভাবে আসতে পারে যেমন ৫+২, ৬+১, ৪+৩, এভাবে
মোট ৬ ভাবে আসতে পারে। এর মানে এর প্রোবাবিলিট ৬/৩৬ = ১/৬ = ০.১৬৬৭
গ্রাফ করলে ব্যাপারটা এরকম দাঁড়াবে

এবার যদি একই কাজটি ৩ টি ছক্কার গুটি নিয়ে করা হয় তাহলে
দেখবেন ৩ এবং ১৮ মোট ১ টি উপায়ে আসতে পারে মানে এদের
প্রোবাবিলিট ১/৬*৬*৬ = ১/২৫৬ কিন্তু ১০ বা ১১ কিন্তু অনেকভাবেই আসতে পারে।
গ্রাফ করলে ব্যাপারটা এমন দাঁড়াবে
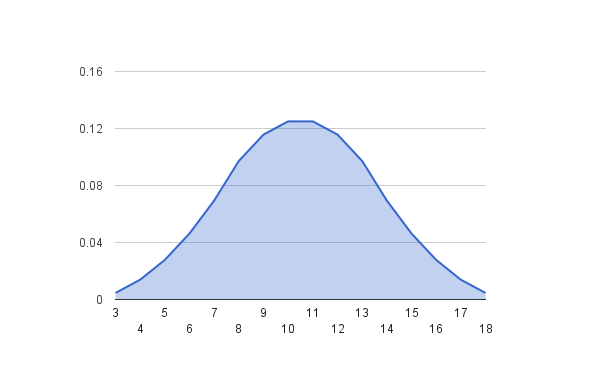
খেয়াল করে দেখুন Distribution এর Shape টা প্রথমে Uniform ছিলো।
Sample Size বাড়ানোর সাথে সাথে এই shape টা
Normal Distribution এর Shape এর মতো হয়ে গেল।
এটাই Central Limit Theorem.
MD. SHAWON SIKDER(SHAKIL)
DEPARTMENT OF STATISTICS
BSMRSTU







0 comments:
Post a Comment